Цветовое пространство XYZ

7.1. ТРЕБОВАНИЯ К ОСНОВНЫМ ЦВЕТАМ XYZ

Практически используемой колориметрической системой служит XYZ, принципы которой в общих чертах были изложены в 5.2.2.

Основные цвета XYZ выбраны для максимального упрощения цветовых расчетов и измерений. Выбор был сделан так, чтобы обеспечить следующие свойства системы.

1. Яркостная характеристика цвета определяется не тремя составляющими цветового уравнения (как в системе RGB, формула 5.4), а только одной (формула 5.5, а).

2. Цветовое уравнение, выражающее любой реальный цвет, включая самые насыщенные — спектральные, не содержит отрицательных координат.

3. При указанных особенностях системы положение белой точки сохраняется в центре треугольника цветности и координаты белого цвета есть Б (1/3; 1/3; 1/3).

4. Одна из цветовых координат большого числа спектральных цветов равняется нулю, и эти цвета, следовательно, выражаются двучленными уравнениями.

Эти свойства связаны с особенностями строения цветового пространства XYZ, которые будут рассмотрены в этой главе. Особое внимание будет уделено плоскости единичных цветов — геометрическому месту точек цветности. Прежде чем рассматривать, каким путем обеспечивались перечисленные здесь особенности системы, необходимо остановиться на некоторых свойствах нереальных цветов.

7.2. НЕРЕАЛЬНЫЕ ЦВЕТА

За пределами площади, ограниченной локусом, располагаются точки цветов, которых нет в природе, — более насыщенных, чем спектральные. Выберем вне поля реаль-

Рис. 7.1. Нереальные цвета на графике r, g

ных цветов точку Г (рис. 7.1) и охарактеризуем цвет, выражаемый ею:

Г= —1,12 R + 0,22G+ 1,90 В.

Единичный цвет Г -- голубой, по цветовому тону тождествен спектральному ?480, но гораздо более насыщен.

Более того, если бы удалось получить излучение воображаемого цвета Г и смешать его с белым, то смесь имела бы цвет монохроматического ?480, включая его насыщенность. Смешивая излучения цветов Г и ?560, можно было бы получить реальный сильно насыщенный С того же цветового тона, что и лежащий между ?480 и ?490.

Можно представить себе и яркость единичного цвета Г. Для этого следует нанести на диаграмму линии яркости и воспользоваться яр-костным масштабом (левая часть рисунка). Воображаемый единичный Г имеет яркость около 0,2 • 680 кд • м~2, а С, полученный сложением воображаемого с реальным, — около 1,5 • 680 кд • м"~2.

Другой пример. Цвет П — пурпурный, дополнительный по цветовому тону к цвету излучения ?560. Смешение излучения нереального цвета П с желто-зеленым ?560 дало бы очень мало насыщенный пурпурный П1. Самое интересное свойство воображаемого цвета П — отсутствие яркости: точка, выражающая этот цвет, лежит на алихне.

7.3. ЦВЕТОВОЙ ТРЕУГОЛЬНИК хуг

Цветовой треугольник хуг создавался на базе цветовой диаграммы rg. На рис. 7.2 она показана вместе с алихной. Выбор основных цветов на этой линии обеспечивает их безъ-яркостность. Так как среди цветов RGB наименьшие яркости имеют В и R, то на алихне выбирают близкие к ним X и Z. Другими словами, сторона хг треугольника хуг должна совпадать с алихной. Третий основной цвет Y обладает яркостью. Его яркостный коэффициент удобно принять равным единице.

Переписав формулу (5.4) в обозначениях системы XYZ, получим Вц

= 680m (xLx + yLv

+ zLz), или, принимая во внимание значения яркости коэффициентов (Lx = 0; Ly = = 1; Lz = 0), BЦ = 680my.

И, следовательно, Вц = 680Y.

Таким образом, первая из целей, поставленных при разработке системы, достигается выбором двух основных цветов на алихне. Подчеркнем, что яркость в системе XYZ определяется поэтому не модулем цвета, как в RGB, а только одной координатой Y.

Достижение второй цели (раздел 7.1) несколько сложнее. Напомним, что цвета, лежащие вне треугольника, имеют отрицательные координаты. Поэтому для того чтобы координаты всех реальных цветов были положительными, локус нужно поместить внутрь треугольника цветности хуг, выбрав должным образом положения его сторон (рис. 7.2). При этом они должны быть расположены достаточно обоснованно и с точки зрения удобства выражения цветов.

В частности, необходимо удовлетворить требования 3 и 4, сформулированные в разделе 7.1.

Обоснуем положение сторон треугольника xyz. Сторона хг, как только что было показано, совпадает с алихной, т.е. отвечает уравнению (6.7): g + 0,208r + 0,013 = 0.

Сторону ху рационально выбрать касательной к локусу.

Этим достигается последняя цель, поставленная при раз-

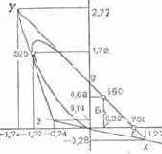
Рис. 7.2. Положение сторон треугольника xyz, найденное расчетным путем

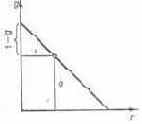
Рис. 7.3. Иллюстрация свойств стороны треугольника, совпадающей с локу-сом

работке системы. При таком выборе все спектральные цвета, которые лежат на этой стороне, описываются Двучленным уравнением

Это видно из рис. 7.3, из которого следует, что для любой точки, лежащей на гипотенузе треугольника rgb, сохраняется равенство r/(1-g) = 1, откуда r + g = 1. Координата z для рассматриваемых цветов равна нулю и, следовательно, составляющая zZ = 0.

Найдем уравнение стороны ху треугольника xyz (рис. 7.2). Из аналитической геометрии известно уравнение прямой, проходящей через две точки:

где индексы 1 указывают координаты первой точки, индексы 2 — координаты второй точки; х и у — текущие координаты.

В наших обозначениях

(7.1)

Выберем две точки на стороне gr. Пусть это одна из точек верхней части прямолинейного участка локуса, например ? = 560 нм и его последняя точка ? = 700 нм. Их координаты приведены на рис. 7.2. Тогда индексы 1 принадлежат координатам точки ?560 (0,32; 0,68), а индексы 2 -координатам точки ?700 (1; 0). Подставляя эти значения в формулу (7.1), получим уравнение стороны ху, совпадающей с прямолинейным участком локуса:

g+r-l=0. (7.2)

Сторона yz выбрана так, чтобы координаты вершин у и z имели следующие значения: у (—1,74; 2,77), z (—0,74; 0,14). При этом указанная сторона почти касается локуса в точке ? = 505 нм. Подставив координаты в формулу (7.1), находим уравнение стороны: g+2,6r+l,8 = 0.

Решая совместно уравнения (6.7) и (7.2), определяют положение вершины х. Учитывая приведенные выше координаты точек у и z, получают (даны уточненные значения)

х (1,2750; —0,2778); у ( — 1,7393; 2,7673); z=( — 0,7431; 0,1409).

Зная две координаты цветности, легко найти третью. Это дает возможность написать следующие уравнения: х= 1,2750 r —0,2778g + 0,0028 b; у = — 1,7393 r + 2,7673 g — 0,0280b; (7.3)

z= —0,7431 r + 0,1409 g + 1,6022b.

Полученный цветовой треугольник показан на- рис. 7.2. Его следует преобразовать, прежде всего, потому, что белая точка не находится в центре треугольника и, следовательно, координаты белого цвета не равны между собой. В этом можно убедиться, найдя сумму х + у + z. Из уравнений (7.3) следует, что суммарный цвет равен Цx+y+z = —1,2074 r + 2,6304 g + 1,5770 b.

Как видно из уравнения, он сильно отличается от белого Напомним, что с подобным случаем мы уже встречались при попытке выразить основные RGB. в обычных единицах яркости. Для того чтобы белая точка заняла в треугольнике rgb центральное положение, потребовалось за единичные количества основных взять разные их яркости, которые, как было указано, находятся в отношении lr : LG : LB = = 1 : 4,59 : 0,06.

Этот же прием применяется и для смещения белой точки в центр треугольника хуг с той только разницей, что задача решается не экспериментально, а путем расчета. Ее решение заключается в том, чтобы найти условия, при которых сумма координат при каждом из основных (уравнения 7.3) равнялась бы единице:

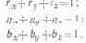
(7.4)

Если указанные суммы равны единице, то Цx+y+z = r + g+b, что и требуется.

Взяв значения координат, входящих в суммы (7.4) из уравнений (7.3), умножим их на постоянные S, Т и U и приравняем суммы единице:

1,2750S — 1./393T —О,7431U=1;

—0,2778 S + 2,7673T + 0,1409 U= 1;

0,0028S—0,0280T+1,6022U = 1.

Тогда получим S = 1,8546; T = 0,5155; U = 0,6299. Умножение каждого из уравнений (7.3) на соответствующий коэффициент дает систему:

Х = 2,36461 R—0,51515G + 0,00520B;

Y=—0,89654 R+1,42640 G —0,01441 В; (7.5)

Z=—0,46807 R + 0,08875 G+1,00921 В.

Поскольку теперь уравнения (7.4) соблюдены, то сумма основных имеет белый цвет.

Уравнения (7.5), связывающие цвета XYZ и RGB, в том виде, в котором они представлены выше, стандартизованы (ГОСТ 13088—67).

Тем не менее они не вполне отвечают одному из требований к основным X, Y, Z. Для иллюстрации этого определим яркостные коэффициенты Lx, Lv, Lz по уравнениям (7.5);

Для того чтобы приравнять LY единице, что было одной из задач, поставленных при разработке системы, уравнения (7.6) делят на 5,65. Тогда формулы перехода превращаются в уравнения (5.6):

X = 0,4185 R—0,0912 G + 0,0009 В; Y= —0,1588 R + 0,2524 G— 0,0025 В; Z = — 0,0829 R + 0,0157 G+0,1786 В.

[Цветовой треугольник хуг, показанный на рис. 7.2, как и треугольник rgb (рис. 6.3), — непрямоугольный. В ре-

Рис. 7.4. Цветовая диаграмма ху; определение доминирующем длины волны основных цветов этой системы зультате его проекционного преобразования (подобном показанному на рис. 6.11) получают прямоугольный треугольник с локусом, находящимся внутри него, — цветовую диаграмму ху (рис. 7.4)

Для наглядности можно цветовые тона основных XYZ представить через доминирующую длину волны. Соединив вершины треугольника с белой точкой, найдем точки пересечения прямых с локусом. Эти точки указывают доминирующую длину волны каждого из основных. Из рисунка

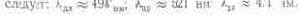
7.4. ОСОБЫЕ ПЛОСКОСТИ В ЦВЕТОВОМ ПРОСТРАНСТВЕ XYZ И ЦВЕТОВАЯ ДИАГРАММА ху

На рис. 7.5 показан проекционно преобразованный в равносторонний треугольник xyz, находящийся в цветовом пространстве этой системы. Так как сторона xz треугольника совпадает с алихной, то координатная плоскость хОг является одновременно и плоскостью нулевых яркостей. Ее иногда, как и линию безъяркостных цветов, называют алихной. В связи с тем что коэффициент LY = 1, координата вершины у равна яр-костной колориметрической единице by = LY • 680 кд x x м-2. Плоскость, параллельная xOz и проходящая через точку у, есть плоскость постоянной яркости, равной В = 680 кд • м-2. Между указанными плоскостями и параллельно им расположены плоскости постоянных яркостей, находящихся между B0 и By (на рисунке не показаны).

Содержание раздела