Однокрасочное растровое изображение

Суммирование ?i

негатива ( на схеме показан как нижний клин) и желтого диапозитива (верхний клин) дает строку матрицы

—0,4 0,3 0,1.

Маска должна компенсировать пурпурную шкалу на желтом негативе. Из рис. 14.28, а или матрицы (14.1) вид­но, что для этой шкалы ?пз= 0,3. Следовательно, аналогич­ный показатель на маске должен равняться ?пз = —0,3. Чтобы получить такую маску, копия совмещенного изобра­жения (рис. 14.28, г) должна быть проявлена до у = 1. Тогда получится маска, отвечающая поставленному требо­ванию (рис. 14.28, д). Результат ее совмещения с маскируе­мым негативом представлен на рис. 14.28, е. Он может быть также выражен строкой матрицы 0,9 0,0 0,1.

Обратим внимание на то, что серая шкала в результате компенсативного маскирования не искажается, а контраст выделяемого изображения не только не падает, но даже воз­растает.

Аналогично рассчитаем маску для пурпурного негати­ва. Строка матрицы диапозитива, сделанного с него:

-0,1 -0,6 -0,3.

Совмещение диапозитива с голубым негативом дает —0,1 —0;5 0,6.

При проявлении до ? = 0,3/0,6 = 0,5 получим

0,05 0,25 —0,3. Результат маскирования:

0,15 0,85 0,0.

Следовательно, матрица цветоделения при компенсатив-ном маскировании в нашем случае имеет вид

0,9 0,0 0,1

0,15 0,85 0,0 (14.1, в)

0,0 0,1 0,9

Т. е. достигнут тот же результат, что и при перекрест­ном маскировании, но при сохранении контраста серой шка­лы.

15.1. ОБЩИЕ СВЕДЕНИЯ О РАСТРОВОМ ВОСПРОИЗВЕДЕНИИ

В разделе 11.2 мы познакомились со стадиями процес­са цветовоспроизведения: цветоделительной, градационной и синтетической.

Техническое оформление цветоделения в разных слу­чаях воспроизведения цветного объекта может быть раз­личным. Например, в полиграфии это — последовательная съемка оригинала через цветоделительные светофильтры. А в цветной фотографии — бесфильтровое экспонирование многослойного цветофотографического материала от объек­та — процесс, основанный на использовании разной зональ­ной чувствительности эмульсионных слоев материала.


Од­нако, несмотря на внешние различия, сущность цветоделе­ния в обоих примерах одна и та же: выделение изображений, образованных зональными составляющими, для последую­щей фотографической регистрации.

Синтетическая стадия в разных способах получения изо­бражений различается уже в большей степени не только по внешним признакам, но и по сущности протекающих явле­ний. В цветной фотографии она состоит в получении совме­щенных сплошных однокрасочных изображений и в резуль­тате этого — в субтрактивном синтезе цветов. При воспро­изведении же оригинала средствами высокой и плоской пе­чати совмещаются дискретные (растровые) изображения, и цвета репродукции образуются путем так называемого авто­типного (от греческого аотост — сам, т. е. без помощи че­ловека, и тьлоа — отпечаток, форма) синтеза. Его за­кономерности связаны со свойствами растрового изображе­ния, которое получается разбиением тонового изображения на мелкие штриховые элементы.

Однако наибольшие различия между полиграфическим и собственно фотографическим воспроизведением приходят­ся на долю градационной стадии процесса. Это связано со следующими обстоятельствами. Во-первых, полиграфиче­ское воспроизведение складывается из большого числа гра­дационных стадий (собственно фотографический процесс, копирование, изготовление форм, печатание), и поэтому здесь вероятность возникновения и накопления градацион­ных искажений особенно велика. Во-вторых, сплошное изображение оригинала преобразуется в растровую репро­дукцию, а ее свойства (а также свойства промежуточных изо­бражений) подчиняются закономерностям растрового про­цесса, отличным от закономерностей обычного тонового. В связи с тем что полиграфическая репродукция растро­вая, при анализе градационной и синтетической стадий не­обходимо принимать во внимание особенности этого вида воспроизведения. Поэтому настоящая глава дает представ­ление об основных свойствах растрового изображения.


В следующей главе, опираясь на эти представления, будут рас­смотрены основные соотношения автотипного синтеза цве­та и особенности градационного процесса при полиграфиче­ском воспроизведении.

При получении оттисков высокой и плоской печати нель­зя создать градацию светлот изменением толщины красоч­ного слоя, так как краска наносится на печатную форму слоем постоянной толщины и так же переносится с формы на бумагу. Поэтому при воспроизведении изображения в полиграфии (кроме глубокой печати) светлотные переходы достигаются в результате разбиения красочного слоя на мелкие штриховые элементы. При этом размеры промежут­ков между штрихами таковы, что указанные элементы на­ходятся на границе зрительного разрешения. Поэтому поле, образованное мелкими штрихами, воспринимается зрительно как светлое, а образованное крупными — как темное. Такие мелкие штрихи будем называть микро­штрихами или растровыми элементами. Для преобразования обычного полутонового изображения в микроштриховое его фотографируют через проекционный или контактный растр (от лат. rastrum — грабли, мотыга). Проекционный растр представляет собой решетку, образо­ванную пересечением непрозрачных линий, а контактный растр — систему закономерно расположенных мелких по­лутоновых элементов, как правило, образующих также род решетки. Кроме того, существуют так называемые нерегулярные растры, решетка которых образована беспорядочно расположенными элементами.

Оптическое изображение оригинала разбивается решет­кой на растровые оптические элементы, составляющие растровое оптическое изображение. Его фотографическая регистрация дает растровое фотографическое изображение, состоящее из микроштриховых элементов, каждый из кото­рых имеет практически постоянную оптическую плотность. Растровый негатив копируют на формный материал, гото­вят печатную форму, а с нее получают растровый оттиск.

Поскольку цветное полиграфическое изображение обра­зовано наложением однокрасочных, то, прежде чем рас­сматривать автотипный синтез, необходимо изучить свойст­ва однокрасочных растровых изображений.



15.2. ФОТОМЕТРИЯ РАСТРОВОГО ИЗОБРАЖЕНИЯ

15.2.1. Общие сведения о фотометрии растрового изображения

Свойства растрового изображения двойственны: с одной стороны, оно дискретно, состоит из отдельных элементов, с другой — должно восприниматься наблюдателем как сплошное. Дискретность дает возможность пользоваться для воспроизведения техникой высокой и плоской печати, а неразличимость элементов позволяет служить оттиску зри­тельным эквивалентом сплошного оригинала.

Двойственность требует введения двух рядов фотомет­рических величин. Свойства изображения как дискретного измеряются растровыми величинами, которые в той или иной форме выражают размеры элементов на оттиске, негативе, позитиве, печатной форме. Свойства изображения как сплошного измеряются визуальными величинами. В послед­нее время для обозначения этого понятия чаще применяют термин «интегральные величины».

Интегральные (визуальные) величины описывают сум­марное (интегральное) действие на глаз штрихов и пробелов данного участка растрового оттиска. Они аналогичны обыч­ным фотометрическим величинам — оптической плотности или коэффициенту пропускания.

В тех случаях, когда хотят подчеркнуть, что величина относится к растровому изображению, ее обозначают сим­волом D? или р?. Однако обычно в индексе нет необходи­мости, и его опускают.

Растровые величины применяются для выражения

свойств главным образом промежуточных растровых изо­бражений -- негативов, диапозитивов, копий, печатных форм. Градационные свойства этих изображений опреде­ляются исключительно площадями элементов, а зрительное впечатление, даваемое ими, играет вспомогательную роль (облегчает контроль изображений).

15.2.2. Растровые величины

Пользуются растровыми величинами двух типов — соб­ственно растровыми величинами и относительными площа­дями растровых элементов. Первые — растровый коэффи­циент пропускания ?R, растровый коэффициент отражения ?R и растровая оптическая плотность DR

— формально тождественны обычным фотометрическим.


Относительные площади растровых элементов обозначают буквой 5.

Собственно растровые величины менее удобны, чем от­носительные площади растровых элементов. Они были вве­дены, чтобы форма оценки фотометрических свойств изо­бражения в растровых процессах была тождественна фор­ме, принятой в обычной фотометрии. Однако усложнения, связанные с этим, не компенсировались преимуществами, состоящими в единообразии формы оценки. В научной и технической литературе чаще пользуются относительными площадями растровых элементов. Тем не менее собственно растровые величины используются еще довольно широко.

Световой поток F0, упавший на растровый участок не­гатива или диапозитива (рис. 15.1), пропорционален его общей площади S, а пропущенный F? — ее части, не заня­той почернением (краской) S — SK:



Это отношение называется растровым коэф­фициентом пропускания.

Растровый коэффициент пропускания (как и другие раст­ровые величины) может служить мерой площади только в том случае, если принять, что поглощение (краска) и про­пускание (пробелы) растрового участка абсолютны. В противном случае F?/F0 ?( S-Sk )/S и понятие теряет смысл.

Для характеристики растрового оттиска служит раст­ровый коэффициент отражения



Величина, выражаемая обратным десятичным лога­рифмом растрового коэффициента пропускания или отраже­ния, называется растровой плотностью:



Если рассматривать не любой растровый участок, а имеющий площадь, равную единице, то приведенные выше формулы приобретают вид





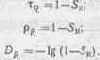
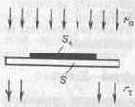
Рис. 15.1. Схема пропуска­ния света растровым участ­ком



Рис. 15.2. Растровая единица площади

Относительные площади растровых элементов. За еди­ницу площади растрового изображения принимается пло­щадка, заключенная между центрами расположенных рядом друг с другом растровых элементов (рис. 15.2). Такая еди­ница площади называется растровой (а также э л е-ментом растра). При измерении площадей растро­вых элементов SК в относительной мере (в растровых еди­ницах) из расчета исключается частота (линиатура) растра.


Если, например, SK = 0,5, то это значит, что половина площади растрового оттиска занята краской. Относитель­ная площадь SK — наиболее употребительная растровая величина. Часто ее измеряют в процентах от общей площади.

Из формулы растровой плотности следует:



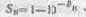
15.2.3. Интегральные (визуальные) величины

Интегральные (визуальные) величины выражают среднее значение коэффициента отражения или оптической плот­ности растрового участка.

Интегральный коэффициент отражения р определяется отношением светового потока Fp, отраженного от растро­вого участка (как от запечатанных его частей, так и от про­белов), к световому потоку F0, упавшему на него. Поток Fp, отраженный от всего участка, равен сумме потоков FK (от краски) и F6 (от бумаги). Следовательно



Тогда интегральная плотность D равна:



15.3. ЗАВИСИМОСТЬ МЕЖДУ ИНТЕГРАЛЬНЫМИ И РАСТРОВЫМИ ВЕЛИЧИНАМИ

15.3.1. Формула Шеберстова—Муррея—Девиса

Интегральная плотность, определяющая уровень зри­тельного ощущения, возникающего при рассматривании растрового участка, связана с размерами растровых эле­ментов.

Чтобы получить на репродукции то или иное распределе­ние визуальных плотностей, ту или иную их градацию, нужно знать, какими площадями элементов обеспечивается заданная интегральная плотность. Если связь между инте­гральной плотностью и площадями элементов известна, то можно рассчитать размеры элементов, обеспечивающие нужную градацию оттиска. Первоначально эта задача была решена для идеализированного растрового процесса, т. е. такого, в котором с целью упрощения соотношений принят ряд допущений. Важнейшие из них: свет не рассеивается в краске и бумаге, краска не впитывается в бумагу. Связь между плотностями и площадями растровых элементов для идеализированного растрового процесса была найдена В. И. Шеберстовым и независимо от него американскими исследователями Мурреем и Девисом.

Световой поток FK, отражаемый краской, находящейся на единичном участке растрового оттиска (рис. 15.3), определяется площадью SK растрового элемента и коэффициен­том отражения рк краски:





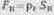
Поток, отражаемый бумагой, пропорционален ее пло­щади, свободной от краски, т. е. 1 — SK, и коэффициенту отражения рб бумаги:



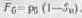
Полное отражение участка растрового изображения на единице площади равно:



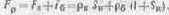
Перейдя от коэффициентов отражения к оптическим плот­ностям, получим



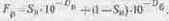
Приняв за единицу поток, упавший на единичный уча­сток (F0 = 1), получим формулу, связывающую интеграль­ную плотность растрового участка оттиска с площадью раст­рового элемента на нем в зависимости от оптической плот­ности бумаги и краски:



Это формула Шеберстова—Муррея—Девиса. Она спра­ведлива только при указанных выше допущениях.

Отсчитав плотность краски от плотности бумаги (т. е.

приняв 10-Dб = 1), получим ее более употребительную форму:



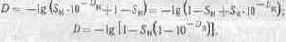
При бесконечно большой оптической плотности краски



где Sn — площади растровых элементов позитива.

Установим форму графика, выражающего функцию Ше­берстова—Муррея—Девиса. Для этого вспомним, что кри­вая у = lg х при 0 < х ? 1 расположена в четвертом квадранте плоскости (рис. 15.4 сплошная линия). При за­мене аргумента на 1 — х кривая зеркально перевернется (штриховая линия). Если, заменив аргумент, изменить знак перед логарифмом на обратный, то отрицательные значе­ния функции станут положительными и получится график,

симметричный предыдущему, но находящийся в первом

квадранте.

Подставив в выражение y=lgx вместо у значения D, авместо х значения S, найдем, что при бесконечно большой оптической плотности краски, когда D = —lg (1 — SK), т. е. 10-DК = 0, формула Шеберстова—Муррея—Девиса выражается верхней кривой семейства, показанного на



Рис. 15.3. Схема пропускания све­та участками растрового оттиска



Рис. 15.4. Логарифмические кривые при 0<x?1



Рис. 15.5, Графическое выражение функции Шеберстова — Муррея — Девиса при разных оптических плотностях краски

рис. 15.5. С уменьшением плотности краски член —SK (1 — — 10~Dк) становится меньше, и кривая опускается.

Наибольшие значения интегральной плотности оттис­ка D равны DK.



15.3.2. Эффект Юла—Нилсена

Экспериментальная проверка формулы Шеберстова— Муррея— Девиса показала, что оптическая плотность раст­рового оттиска в действительности оказывается большей, чем следует из этой формулы. Юл и Нилсен, изучавшие за­висимость между D и SK, объяснили экспериментально на­блюдаемое отклонение тем, что свет, упавший на пробельные участки оттиска, не только отражается ими, но и про­ходит в бумагу, рассеивается там, и некоторая доля этой рассеянной составляющей поглощается краской растровых элементов. Схематически явление показано на рис. 15.6. Световой пучок /, направленный на растровое изображение, оттиснутое на бумажной подложке, частично отражается от поверхности бумаги (составляющая 2), а частично проникает в ее толщу, рассеивается волокнами целлюлозы и в извест­ной степени поглощается краской при выходе из бумаги. На рис. 15.6 из множества рассеивающих частиц выделена только одна, обозначенная буквой А. Таким образом, свет претерпевает дополнительное поглощение, не предусмот­ренное формулой Шеберстова—Муррея—Девиса, что и объясняет несоответствие фактической плотности растро­вого участка этой формуле.

Эффект дополнительного поглощения света краской иногда называется краевым, так как он особенно заметен вблизи границы пробела с запечатанным участком.

Юл и Нилсен предложили ввести в формулу Шеберсто­ва—Муррея—Девиса поправку в виде коэффициента п, учитывающего краевой эффект светорассеяния, а также не­которые другие явления, и в частности поглощение света в толще бумаги. Формула, предложенная Юлом и Нилсеном, имеет вид



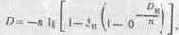
Коэффициент п, стоящий перед знаком логарифма, по­казывает, как возрастает плотность растрового участка вследствие краевого эффекта светорассеяния, а входящий в показатель степени — уменьшение оптической плотности краски из-за того, что она пропускает часть рассеянного света. Во втором случае этот коэффициент меньше влияет на интегральную плотность участка, чем в первом, так как площадь SK входит в сумму, находящуюся под знаком ло­гарифма.


Содержание раздела

---

---