Разрядный двоичный сумматор
Рисунок 1.1. 8-разрядный двоичный сумматор
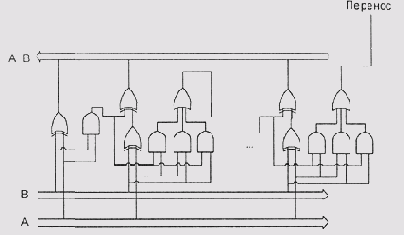
Дополнительный, 9-й разряд, образующийся при сложении 8-разрядных чисел, переносится в специальный бит слова состояния процессора, который также называется битом переноса, и обычно обозначается буквой С (от англ, саrrу — перенос). Этот бит можно использовать как условие в командах условного перехода, а также для реализации 16-разрядной операции сложения или одноименной операции большей разрядности на 8-разрядном АЛУ.
При операциях над беззнаковыми (неотрицательными) числами бит переноса можно интерпретировать как признак переполнения: т. е. того, что результат нельзя представить числом с разрядностью АЛУ. Игнорирование этого бита может приводить к неприятным последствиям: например, складывали мы 164 + 95, а получили в результате 3.
Иногда этот эффект, называемый "оборачиванием счетчиков", имеет и полезное применение. Например, используя "часовой" кварцевый генератор с частотой 32 768 Гц и 15-разрядный двоичный счетчик, мы можем отмерять секунды по появлению бита переноса в 16-м разряде и избавляемся от необходимости сбрасывать сам счетчик.
Двоичное вычитание может выполняться аналогичным образом, только необходимо использовать не таблицы сложения, а таблицы вычитания для двух и трех слагаемых. Не утомляя себя и читателя выписыванием этих таблиц, скажем сразу, что операция двоичного вычитания эквивалентна операции двоичного сложения уменьшаемого с двоичным дополнением вычитаемого. Двоичное дополнение строится таким образом: все биты числа инвертируются (нули заменяются на единицы, и наоборот), а затем к результату добавляется единица. Доказательство этого утверждения мы оставляем любопытному читателю, а сами просто рассмотрим пример 1.2.
[Www cs hut fi SSH]; в протоколе
[www.cs.hut.fi SSH]; в протоколе виртуальных приватных сетей IPSEC время жизни ключа ограничено восемью часами [redbooks.ibm.com sg245234.pdf].
Еще более широкое применение двухключевые схемы нашли в области аутентификации и электронной подписи. Электронная подпись представляет собой контрольную сумму сообщения, зашифрованную приватным ключом отправителя. Каждый обладатель соответствующего публичного ключа может проверить аутентичность подписи и целостность сообщения. Это может использоваться для проверки аутентичности как сообщения, так и самого отправителя. Использование в качестве контрольной суммы обычного CRC (см. разд. Контрольные суммы) невозможно, потому что генерация сообщения с заданным CRC не представляет вычислительной сложности. Для применения в электронной подписи были разработаны специальные алгоритмы вычисления контрольных сумм, затрудняющие подбор сообщения с требуемой суммой [RFC 1320, RFC 1321].
[Www distributed net]!
[www.distributed.net]!
Простым и эффективным способом борьбы с такой атакой является расширение пространства ключей. Увеличение ключа на один бит приводит к увеличению пространства вдвое -- таким образом, линейный рост размера ключа обеспечивает экспоненциальный рост стоимости перебора. Некоторые алгоритмы шифрования не зависят от разрядности используемого ключа—в этом случае расширение достигается очевидным способом. Если же в алгоритме присутствует зависимость от разрядности, расширить пространство можно, всего лишь применив к сообщению несколько разных преобразований, в том числе и одним алгоритмом, но с разными ключами. Еще один способ существенно усложнить работу взломщику — это упаковка сообщения перед шифрованием и/или дополнение его случайными битами.
Важно подчеркнуть, впрочем, что количество двоичных разрядов ключа является лишь оценкой объема пространства ключей сверху, и во многих ситуациях эта оценка завышена. Некоторые алгоритмы в силу своей природы могут использовать только ключи, удовлетворяющие определенному условию — например, RSA использует простые Числа. Это резко сужает объем работы по перебору, поэтому для обеспечения сопоставимой криптостойко-сти разрядность ключа RSA должна быть намного больше, чем у алгоритмов, допускающих произвольные ключи.
Низкая криптостойкость может быть обусловлена не только алгоритмом шифрования, но и процедурой выбора ключа: если ключ может принимать любые двоичные значения заданной разрядности, но реально для его выбора используется страдающий неоднородностью генератор псевдослучайных чи-:ел, мы можем значительно сократить объем пространства, которое реально аолжен будет перебрать взломщик наших сообщений (вопросы генерации завномерно распределенных псевдослучайных чисел обсуждаются во втором гоме классической книги [Кнут 2000]). Еще хуже ситуация, когда в качестве ключа используются "легко запоминаемые" слова естественного языка: в этом случае реальный объем пространства ключей даже довольно большой разрядности может измеряться всего лишь несколькими тысячами различных значений.
Современные алгоритмы шифрования делятся на два основных класса: с секретным и с публичным ключом (кажущееся противоречие между термином "публичный ключ" и приведенными выше рассуждениями будет разъяснено далее).
Алгоритмы- с секретным ключом, в свою очередь, делятся на потоковые (stream) и блочные (block). Потоковые алгоритмы обычно используют подстановку символов без их перестановки. Повышение криптостойкости при этом достигается за счет того, что правила подстановки зависят не только от самого заменяемого символа, но и от его позиции в потоке.
Примером простейшего — и в то же время абсолютно не поддающегося взлому — потокового алгоритма является система Вернама или одноразовый блокнот (Рисунок 1.10). Система Вернама основана на ключе, размер которого равен размеру сообщения или превосходит его. При передаче двоичных данных подстановка осуществляется сложением по модулю 2 (операцией исключающего или) соответствующих битов ключа и сообщения.
[Www rsa com FAQ]
[www.rsa.com FAQ].
Известные двухключевые алгоритмы требуют соответствия ключей весьма специфическим требованиям, поэтому для достижения криптостойкости, сопоставимой с блочными алгоритмами, необходимо использовать ключи намного большей разрядности. Так, снятые в 2000 году ограничения Министерства торговли США устанавливали ограничения разрядности ключа, который мог использоваться в экспортируемом за пределы США программном обеспечении: для схем с секретным ключом устанавливался предел, равный 48 битам, а для схем с открытым — 480.
Использование ключей большой разрядности требует значительных вычислительных затрат, поэтому двухключевые схемы чаше всего применяются в сочетании с обычными: обладатель публичного ключа генерирует случайную последовательность битов, кодирует ее и отправляет обладателю приватного ключа. Затем эта последовательность используется в качестве секретного ключа для шифрования данных. При установлении двустороннего соединения стороны могут сначала обменяться своими публичными ключами, а затем использовать их для установления двух разных секретных ключей, используемых для шифрования данных, передаваемых в разных направлениях.
Такая схема делает практичной частую смену секретных ключей: так, в протоколе SSH ключ генерируется на каждую сессию
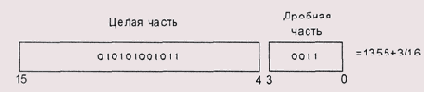
Число с двоичной фиксированной точкой
Рисунок 1.3. Число с двоичной фиксированной точкой
Примечание
Примечание
В русском языке принято называть разделитель целой и дробной частей позиционной дроби запятой, а в английском — точкой. Современная вычислительная терминология формировалась на английском языке, и английские словосочетания fixed-point и floating-point часто переводились на русский язык буквально, поэтому словосочетания "фиксированная точка" и "плавающая точка" прочно вошли в русскую компьютерную лексику, и мы будем использовать именно их.
Современные процессоры обычно не предоставляют арифметических операций с фиксированной точкой, однако никто не запрещает программисту или разработчику компилятора реализовать такие операции на основе стандартных целочисленных операций и команд битового сдвига.
Если нам необходима точность вычислений, определенная количеством десятичных знаков (например, при подсчете рублей с точностью до копеек), нужно помнить, что большинство десятичных дробей в позиционной двоичной записи представляют собой периодические (с бесконечным числом знаков) дроби. Для обеспечения требуемой точности нам следует либо иметь дополнительные двоичные позиции, либо вместо фиксированной двоичной использовать фиксированную десятичную точку: складывать такие числа по-прежнему можно с помощью целочисленных операций, но коррекцию умножения и деления необходимо выполнять с помощью умножения (деления) на степень десяти, а не на степень двойки.
В научных и инженерных вычислениях и цифровой обработке сигналов шире применяются числа с плавающей двоичной точкой. Дело в том, что исходные данные для таких вычислений обычно являются результатами измерений физических величин. Все физически реализуемые способы измерений сопровождаются ошибками: для объяснения этого печального факта часто ссылаются на принцип неопределенности Гейзенберга [Карнап 1971], но при практических измерениях гораздо большую роль играют следующие виды ошибок.
Если с принципом Гейзенберга бороться невозможно, то тепловые и инструментальные ошибки можно уменьшать, первые — снижением температу-Pbi, а вторые — большей тщательностью изготовления и калибровки, ужесточением условий эксплуатации и хранения или совершенствованием самого инструмента (например, интерферометрический лазерный дальномер при равной тщательности изготовления будет намного точнее рулетки).
Однако ни абсолютный нуль температуры, ни абсолютная точность изготовления физически недостижимы, и даже приближение к ним в большинстве ситуаций недопустимо дорого.
Сомневающемуся в этом утверждении читателю предлагается представить, во что бы превратилась его жизнь, если бы при взвешивании продуктов в магазине сами продукты и весы охлаждались хотя бы до температуры жидкого азота, а плотницкий метр надо было бы хранить с теми же предосторожностями, что и метрологический эталон.
Поэтому на практике целесообразно смириться с погрешностями измерений, а на приборе указать точность, которую его изготовитель реально может гарантировать при соблюдении пользователем условий хранения и эксплуатации. Полному искоренению подлежат только методологические ошибки, да и с ними во многих ситуациях приходится смириться из-за неприемлемо высокой стоимости прямых измерений.
Относительно дешевый способ повышения точности — многократные измерения и усреднение результата, но этот метод повышает стоимость измерений и, если измерения производятся одним и тем же инструментом, не позволяет устранить инструментальные и методологические ошибки.
И тепловые шумы, и инструменты порождают ошибки, которые при прочих равных условиях пропорциональны измеряемой величине. Десяти метровая рулетка имеет инструментальную ошибку, измеряемую миллиметрами, а десятисантиметровый штангенциркуль — микронами. Поэтому ошибку измерений часто указывают не в абсолютных единицах, а в процентах.
При записи результатов измерений хорошим тоном считается указывать точность этих измерений и не выписывать десятичные цифры (или знаки после запятой), значения которых лежат внутри границ ошибки. Цифры перед десятичной запятой в этом случае заменяются нулями, а после нее -просто отбрасываются. Для сокращения записи больших значений, измеренных с относительно небольшой точностью, в научной и инженерной литературе используется экспоненциальная запись чисел: незначащие (в данном случае — лежащие внутри границ ошибки) младшие десятичные цифры отбрасываются, и после числа добавляется 10N, где N — количество отброшенных цифр. Обычно рекомендуют нормализовать такую запись, перемещая десятичную запятую на место после старшей цифры (смещение запятой на одну позицию влево соответствует увеличению показателя степени множителя на единицу). В соответствии с этими правилами величина 2128506 ± 20 преобразуется к виду 2,12850х106 (обратите внимание, что младший ноль в данном случае является значащим).
При бытовых измерениях обычно обходятся двумя-тремя значащими десятичными цифрами. В научных и инженерных измерениях используются и большие точности, но на практике измерения с точностью выше шестого десятичного знака встречаются разве что при разработке и калибровке метрологических эталонов. Для сравнения, цифровая телефония обходится 8-ю битами, а аналого-цифровой преобразователь бытовой звуковой карты имеет 12, реже 14 значащих двоичных разрядов. Большинство современных карт считаются 16-битными, но на практике младшие разряды их АЦП оцифровывают только тепловой шум усилителя и собственных старших разрядов, а также ошибки калибровки того и другого. Честные (т. е. такие, у которых все разряды значащие) 16-разрядные АЦП используются в профессиональной звукозаписывающей и измерительной аппаратуре, 24-разрядные АЦП относятся к прецизионной аппаратуре, а 32-разрядные на практике не применяют.
Вычислительные системы широко используют представления чисел с плавающей точкой, только не десятичной, а двоичной (Рисунок 1.4). Идея этого представления состоит в том, чтобы нормализовать позиционную двоичную дробь, избавившись от незначащих старших нулевых битов и освободив место для [возможно] значащих младших разрядов. Сдвиг, который нужен для нормализации, записывается в битовое поле, называемое порядком. Само же число называется мантиссой.
Число с плавающей двоичной точкой
Рисунок 1.4. Число с плавающей двоичной точкой

Число с плавающей точкой, таким образом, состоит из двух битовых полей — мантиссы М и порядка Е. Число, представленное двумя такими полями, равно Мх2Е. Нормализация состоит в отбрасывании всех старших нулей, поэтому старший бит нормализованной двоичной мантиссы всегда равен 1. Большинство современных реализаций чисел с плавающей точкой используют этот факт для того, чтобы объявить незначащими не только старшие нули, но и эту единицу, и, таким образом, выигрывают дополнительный бит точности мантиссы.
Сложение двух чисел с плавающей точкой состоит в денормализации мантисс (совмещении двоичных точек), их сложении и нормализации результата. Перемножение таких чисел, соответственно, выполняется перемножением мантисс, сложением порядков и опять-таки нормализацией результата.
В некоторых старых архитектурах, например БЭСМ-6, все арифметические операции выполнялись над числами с плавающей точкой, однако существовала возможность выключить нормализацию мантиссы. Ненормализованные числа с плавающей точкой использовались для представления значений с фиксированной точкой, в том числе и целочисленных.
Стандарт языка ANSI С требует наличия 32-битового (8-разрядный порядок и 24-разрядная мантисса) и 64-битового (16-разрядный порядок и 48-разрядная мантисса) представлений чисел с плавающей точкой, которые называются, соответственно, числами одинарной и двойной точности (float и double float или просто double). Числа двойной точности, конечно же, не могут быть результатом прямых измерений физических величин, но позволяют избежать накопления ошибок округления при вычислениях.
Большинство современных процессоров общего назначения и ориентированных на приложения цифровой обработки сигналов (ЦОС) предоставляет операции над такими числами, а зачастую и над числами большей разрядности. Операции практически всегда включают сложение, вычитание, умножение и деление. Часто на уровне системы команд реализуются и элементарные функции: экспонента, логарифм, квадратный корень, синус, косинус и т. д. Процессоры ЦОС нередко предоставляют и отдельные шаги дискретного преобразования Фурье.
Количество операций с плавающей точкой в секунду (Floating Operations Per Second, FLOPS, в наше время чаше говорят о Mflops — миллионах операций в секунду), которые может исполнять процессор, является одной из важных его характеристик, хотя и не для всех приложений эта характеристика критична.
Двоичнодесятичное представление чисел
Рисунок 1.2. Двоично-десятичное представление чисел
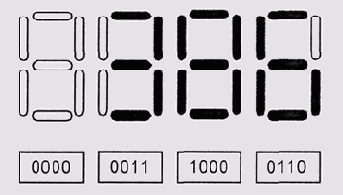
Вместо арифметических операций над такими числами большинство современных микропроцессоров предлагают использовать для их сложения и вычитания обычные бинарные операции, а потом исправлять возникающие при этом недопустимые значения при помощи специальной команды двоично-десятичной коррекции. Алгоритм работы этой команды читателю предлагается разработать самостоятельно. Для него потребуется информация о том, происходил ли при сложении двоичный перенос из младшей тетрады. Процессоры, предоставляющие такую команду, имеют и бит межтетрадного переноса.
Если операция производится над числами, имеющими 16 или более двоичных разрядов (4 и более двоично-десятичных), для коррекции нам недостаточно одного межтетрадного переноса — надо иметь по биту переноса на каждую из пар последовательных тетрад. Так далеко ни один из существующих процессоров не заходит. Например, 32-разрядные процессоры х86 имеют команды двоично-десятичной коррекции только для операций над числами с 8-ю двоичными (двумя двоично-десятичными) разрядами.
Двухмерное векторное изображение
Рисунок 1.5. Двухмерное векторное изображение

Каждый примитив описывается своими геометрическими координатами. Точность описания в разных форматах различна, нередко используются числа с плавающей точкой двойной точности или с фиксированной точкой и точностью до 16-го двоичного знака.
Координаты примитивов бывают как двух-, так и трехмерными. Для трехмерных изображений, естественно, набор примитивов расширяется, в него включаются и различные поверхности — сферы, эллипсоиды и их сегменты, параметрические многообразия и др. (Рисунок 1.6).
Контрольные суммы
Контрольные суммы
Хранение данных и их передача часто сопровождается или может сопровождаться ошибками. Приемнику и передатчику информации необходимо знать, что данные в потоке должны соответствовать определенным правилам. Приводя реальный поток в соответствие с этими правилами, приемник может восстановить его исходное содержание. Количество и типы практически восстановимых ошибок определяются применяемыми правилами кодирования. Понятно, что всегда существует (и во многих случаях может быть теоретически оценен) порог количества ошибок в сообщении, после которого сообщение не поддается даже частичному восстановлению.
Соответствие потока данных тем или иным правилам теория информации описывает как наличие статистических автокорреляций или информационной избыточности в потоке. Такие данные всегда будут иметь больший объем, чем эквивалентные, но не соответствующие никаким правилам (например, упакованные), т. е. помехозащищенность достигается не бесплатно. Существование "бесплатных" средств повышения помехозащищенности каналов противоречит, ни много, ни мало, Второму Началу термодинамики (доказательство этого утверждения требует глубоких знаний в области теории информации и термодинамики, и поэтому здесь не приводится).
Естественные языки обеспечивают очень высокую (в письменной форме Двух- и трехкратную, а в звуковой еще большую) избыточность за счет применения сложных фонетических, лексических и синтаксических правил. Остроумным способом дополнительного повышения избыточности человеческой речи являются стихи (белые и, тем более, рифмованные), широко использовавшиеся до изобретения письменности для повышения надежности хранения в человеческих же головах исторических сведений и священных текстов.
К сожалению, с задачей восстановления искаженных сообщений на естественных языках в общем случае может справиться лишь человеческий мозг. Правила кодирования, применимые в вычислительных системах, должны удовлетворять не только требованиям теоретико-информационной оптимальности, но и быть достаточно просты для программной или аппаратной реализации.
Простейшим способом внесения избыточности является полное дублирование данных. Благодаря своей простоте, этот способ иногда применяется ни практике, но обладает многочисленными недостатками. Во-первых, избыточность этого метода чрезмерно высока для многих практических применений. Во-вторых, он позволяет только обнаруживать ошибки, но не исправлять их: при отсутствии других правил кодирования, мы не можем знать, какая из копий верна, а какая ошибочна.
Троекратное копирование обеспечивает еще более высокую избыточность, зато при его использовании для каждого расходящегося бита мы можем проводить голосование: считать правильным то значение, которое присутствует минимум в двух копиях данных (в данном случае мы исходим из того, что вероятность ошибки в одном и том же бите двух копий достаточно мала).
Трехкратное копирование, таким образом, позволяет восстанавливать данные, но имеет слишком уж высокую избыточность. Эти примеры, кроме простоты, любопытны -тем, что демонстрируют нам практически важную классификацию избыточных кодов: бывают коды, которые только обнаруживают ошибки, а бывают и такие, которые позволяют их восстанавливать. Далеко не всегда коды второго типа могут быть построены на основе кодов первого типа. Во многих случаях, например при передаче данных по сети, целесообразно запросить повтор испорченного пакета, поэтому коды, способные только обнаруживать ошибки, практически полезны и широко применяются.
Все данные, с которыми могут работать современные вычислительные системы, представляют собой последовательности битов, поэтому все правила, которые мы далее будем рассматривать, распространяются только на такие последовател ьности.
Простейший из применяемых способов кодирования с обнаружением ошибок — это бит четности. Блок данных снабжается дополнительным битом, значение которого выбирается так, чтобы общее количество битов, равных единице, в блоке было четным. Такой код позволяет обнаруживать ошибки в одном бите блока, но не в двух битах (строго говоря — позволяет обнаруживать нечетное количество ошибочных битов). Если вероятность ошибки в двух битах достаточно велика, нам следует либо разбить блок на два блока меньшего размера, каждый со своим битом четности, либо использовать более сложные схемы кодирования.
Самая распространенная из таких более сложных схем — это CRC (Cyclic Redundancy Code, циклический избыточный код). При вычислении CRC разрядности N выбирают число R требуемой разрядности и вычисляют остаток от деления на R блока данных (рассматриваемого как единое двоичное число), сдвинутого влево на N битов. Двоичное число, образованное блоком данных и остатком, делится на R, и этот факт можно использовать для проверки целостности блока (но не для восстановления данных при ошибке!).
Способность контрольной суммы обнаруживать ошибки логичнее измерять не в количестве ошибочных битов, а в вероятности необнаружения ошибки. При использовании CRC будут проходить незамеченными лишь сочетания ошибок, удовлетворяющие весьма специальному условию, а именно такие, вектор ошибок (двоичное число, единичные биты которого соответствуют ошибочным битам принятого блока, а нулевые — правильно принятым) которых делится на R. При случайном распределении ошибок вероятность этого может быть грубо оценена как 1/R, поэтому увеличение разрядности контрольной суммы в сочетании с выбором простых R обеспечивает достаточно быстрый и дешевый способ проверки целостности даже довольно длинных блоков. 32- разрядный CRC обеспечивает практически полную гарантию того, что данные не были повреждены, а 8-разрядный — уверенность, достаточную для многих целей. Однако ни четность, ни CRC не могут нам ничем помочь при восстановлении поврежденных данных.
Простой метод кодирования, позволяющий не только обнаруживать, но и исправлять ошибки, называется блочной или параллельной четностью и состоит в том, что мы записываем блок данных в виде двухмерной матрицы и подсчитываем бит четности для каждой строки и каждого столбца. При одиночной ошибке, таким образом, мы легко можем найти бит, который портит нам жизнь. Двойные ошибки такая схема кодирования может обнаруживать, но не способна восстанавливать (Рисунок 1.9).
Параллельная четность
Рисунок 1.9. Параллельная четность

Широко известный и применяемый код Хэмминга (Hamming code) находится в близком родстве с параллельной четностью. Его теоретическое обоснование несколько менее очевидно, чем у предыдущего алгоритма, но в реализации он, пожалуй, даже проще [Берлекэмп 1971]. Идея алгоритма состоит в том, чтобы снабдить блок данных несколькими битами четности, подсчитанными по различным совокупностям битов данных. При выполнении неравенства Хэмминга (1.1) сформированный таким образом код обеспечивает обнаружение и исправление одиночных ошибок либо гарантированное обнаружение (но не исправление!) двойных ошибок. Важно подчеркнуть гарантию обнаружения, в отличие от всего лишь высокой вероятности обнаружения при использовании CRC.
d + р+1<= 2р, (1.1)
где d — количество битов данных, р — разрядность контрольного кода.
Код, использующий d и р, при которых выражение (1.1) превращается в равенство, называют оптимальным кодом Хэмминга.
Часто оказывается целесообразно сочетать упаковку данных с их избыточным кодированием. Наиболее удачным примером такой целесообразности опять-таки являются тексты на естественных языках: статистический анализ такого текста показывает очень высокий, более чем двукратный, уровень избыточности. С одной стороны, это слишком "много для большинства практически применяемых способов цифровой передачи и кодирования данных, а с другой — правила формирования этой избыточности слишком сложны и плохо формализованы для использования в современных программно-аппаратных комплексах. Поэтому для длительного хранения или передачи по низкоскоростным линиям целесообразно упаковывать текстовые данные и снабжать их простыми средствами избыточности, например CRC.
Представление данных в вычислительных системах
Представление данных в вычислительных системах
Из курсов компьютерного ликбеза известно, что современные компьютеры оперируют числовыми данными в двоичной системе счисления, а нечисловые данные (текст, звук, изображение) так или иначе переводят в цифровую форму (оцифровывают).
В силу аппаратных ограничений процессор оперирует числами фиксированной разрядности. Количество двоичных разрядов основного арифметико-логического устройства (АЛУ) называют разрядностью процессора (впрочем, ниже мы увидим примеры, когда под разрядностью процессора подразумевается и нечто другое). Процессоры современных систем коллективного пользования (z90, UltraSPARC, Alpha) имеют 64-разрядные АЛУ, хотя в эксплуатации остается еще довольно много 32-разрядных систем, таких, как System/390. Персональные компьютеры (х86, PowerPC) и серверы рабочих групп имеют 32-разрядные процессоры. Процессоры меньшей разрядности — 16-, 8- и даже 4-разрядные — широко используются во встраиваемых приложениях.
В прошлом встречались и процессоры, разрядность которых не являлась степенью числа 2, например 36- или 48-разрядные, но из-за сложностей переноса программного обеспечения и обмена данными между системами с некратной разрядностью такие машины постепенно вымерли.
Представление изображений
Представление изображений
Все известные форматы представления изображений (как неподвижных, так и движущихся) можно разделить на растровые и векторные.
В векторном формате изображение разделяется на примитивы -- прямые линии, многоугольники, окружности и сегменты окружностей, параметрические кривые, залитые определенным цветом или шаблоном, связные области, набранные определенным шрифтом отрывки текста и т. д. (Рисунок 1.5). Для пересекающихся примитивов задается порядок, в котором один из них перекрывает другой. Некоторые форматы, например, PostScript, позволяют задавать собственные примитивы, аналогично тому, как в языках программирования можно описывать подпрограммы. Такие форматы часто имеют переменные и условные операторы и представляют собой полнофункциональный (хотя и специализированный) язык программирования.
Представление рациональных чисел
Представление рациональных чисел
| — Чему равна лошадиная сила? — Это сила лошади весом один килограмм и ростом один метр —Да где же вы видели такую лошадь? — А ее вообще мало кто видел. Она хранится под аргоновый колпаком в Палате мер и весов под Парижем. |
Представить произвольное вещественное число при помощи конечного числа элементов, способных принимать лишь ограниченный набор значений (а именно таковы все цифровые представления данных), разумеется, невозможно. Максимум, что можно сделать — это найти то или иное рациональное приближение для такого числа, и оперировать им.
Примечание
Примечание
На самом деле, возможно точное, а не приближенное представление вещественных чисел рациональными — не одиночной дробью, а сходящейся бесконечной последовательностью дробей, так называемое Гильбертово сечение. Конечным представлением служит не сама последовательность, а правило ее формирования. Из-за своей сложности такое представление крайне редко используется в вычислительных системах и никогда не реализуется аппаратно.
Два основных представления рациональных чисел, используемых в компьютерах, — это представления с фиксированной и плавающей точкой. Интерпретирующие системы (например, MathCAD) иногда реализуют и собственно рациональные числа, представляемые в виде целых числителя и знаменателя, но процессоры, умеющие работать с такими числами на уровне системы команд, автору неизвестны.
Представление с фиксированной точкой (Рисунок 1.3) концептуально самое простое: мы берем обычное двоичное число и объявляем, что определенное количество его младших разрядов представляет собой дробную часть в позиционной записи. Сложение и вычитание таких .чисел может выполняться при помощи обычных целочисленных команд, а вот после умножения и перед делением нам надо, так или иначе, передвинуть двоичную запятую на место.
Представление текстовых данных
Представление текстовых данных
| Вы можете прочитать третью снизу строку таблицы? — Н, К, И, М... Доктор, у вас криво настроена кодировка! |
Все используемые способы представления текстовых данных, так или иначе, сводятся к нумерации символов алфавита (или множества символов системы письменности интересующего нас языка, которое используется вместо алфавита — слоговой азбуки, иероглифов и т. д.) и хранения полученных целых чисел наравне с обычными числами. Способ нумерации называется кодировкой, а числа — кодами символов.
Для большинства кодировок языков, использующих алфавитную письменность (латиница, кириллица, арабский алфавит, еврейский и греческий языки) достаточно 127 символов. Самая распространенная система кодирования латиницы — ASCII — использует 7 бит на символ. Другие алфавиты обычно кодируются более сложным образом: символы алфавита получают коды в диапазоне от 128 до 255, а коды от 0 до 127 соответствуют кодам ASCII. Таким образом, любой символ этих алфавитов, в том числе и в многоязычных текстах, использующих сочетание национального алфавита и латиницы, может быть представлен 8-ю битами или одним байтом. Но для японских слоговых азбук, а тем более для китайской иероглифики, 255 кодов явно
недостаточно, и приходится использовать многобайтовые кодировки. Распространенное обозначение таких кодировок — DBCS (Double Byte Character Set — набор символов, кодируемый двумя байтами).
Двух байтов, в принципе, достаточно, чтобы сформировать единую кодировку для всех современных алфавитов и основных подмножеств иерогли-фнки. Попытка стандартизовать такое представление — Unicode — пока что не имеет полного успеха. Отчасти это можно объяснить тем, что потребность в представлении разноязыких текстов в пределах одного документа ограничена, кроме того, слишком много старого программного обеспечения использует предположение о том, что символ занимает не более байта. Такие программы не могут быть легко преобразованы для работы с Unicode.
Используются две основные кодировки латиницы -- ASCII и EBCDIC (Extended Binary Coded Decimal Information Code), применяемая системами AS/400, System/370, System/390 и z90 фирмы IBM. Для представления русского варианта кириллицы существует три основных кодировки: альтернативная (известная также как ср866), ср!251 и KOI-8 и ряд менее широко используемых (ISO 8892-5 и др.).
Арифметические операции над такими "числами" обычно бессмысленны, зато большой смысл имеют операции сравнения. Операции сравнения в современных процессорах реализованы как неразрушающее вычитание — мы производим те же действия, что и при обычном двоичном вычитании, но запоминаем не сам результат, а лишь флаги знака, переноса и равенства результата нулю. На основании значений этих флагов определяем результат сравнения: если разность равна нулю, сравниваемые символы одинаковы, если она положительна или отрицательна, один из символов больше или меньше другого.
Естественно, чаще всего мы хотим интерпретировать результаты посимвольного сравнения как лексикографическое (алфавитное) "больше" или "меньше" (для русского алфавита, "а" меньше, чем "б"). Проще всего это делать, если нумерация символов совпадает с их порядком в алфавите, но далеко не для всех распространенных кодировок это справедливо.
В кодировке ASCII (American Standard Code for Information Interchange — Американский стандартный код обмена информацией), например, все символы латиницы, цифры и большинство распространенных знаков препинания обозначаются кодами от 0 до 127, при этом коды букв расставлены в соответствии с латинским алфавитом. В США, как и в других англоязычных странах, латинский алфавит используется в неизмененном виде, а для передачи звуков, отсутствовавших в оригинальном латинском языке, применяется причудливая орфография. Большинство других европейских алфавитов обходит проблему несоответствия фонетик путем расширения набора символов латиницы — например, в немецком языке добавлены буквы ö, ä, ü и ß. Другие языки имеют множество различных "акцентов" и "диакритических символов", расставляемых над буквами для указания особенностей произношения. Некоторые языки, например французский, используют одновременно и расширения алфавита, и причудливую орфографию. Нередко встречаются и дополнительные знаки препинания, например, ¿ и ¡ в испанском языке.
Все символы-расширения в каждом из национальных алфавитов находятся на определенных местах, но при использовании кодировки ASCII для представления этих символов сохранить этот порядок невозможно — соответствующие коды уже заняты. Так, в кодировке ISO 8895-1 все символы латиницы кодируются в соответствии с ASCII, а коды расширений более или менее произвольно раскиданы между 128 и 255. Более яркий пример той же проблемы — кодировки кириллицы семейства KOI, в которых символы кириллицы сопоставлены фонетически соответствующим им символам латиницы (филе нот фоунд, или, наоборот, esli wy не movete pro^itatx eto po-russki, smenite kodirovku). Естественно, совместить такое сопоставление и алфавитную сортировку невозможно.
Стандартным решением в таких случаях является использование для сравнения и лексикографической сортировки промежуточных таблиц, в которых для каждого допустимого кода указан его номер в лексикографическом порядке. На уровне системы команд процессоры этого обычно не делают, но на уровне библиотек языков высокого уровня это осуществляется очень часто.
При обмене данными между системами, использующими разные кодировки, необходимо учитывать этот факт. Стандартный способ такого учета, применяемый во многих кросс-платформенных форматах документов (HTML, MIME) — это сообщение где-то в теле документа (обычно в его начале) или в передаваемой вместе с документом метаинформации об используемых языке и кодировке. Большинство средств просмотра почты и документов HTML умеют интерпретировать эту метаинформацию, поэтому конечный пользователь все реже и реже сталкивается с необходимостью самостоятельно разбираться в различных кодировках.
Проблемы возникают, когда метаинформация не указана или, что еще хуже, указана неправильно. Последнее особенно часто встречается при неправильной настройке почтового клиента у отправителя. Для борьбы с такими сообщениями разработаны даже специальные программы, применяющие частотный анализ текста для определения реально использованной кодировки.
Два основных подхода к представлению форматированного текста — это языки разметки и сложные структуры данных, используемые в текстовых процессорах. Примерами языков разметки являются HTML, LATEX, troff. В этих языках обычный текст снабжается командами, указывающими на то, каким шрифтом следует отображать конкретный фрагмент текста и как его следует форматировать (например, какова ширина параграфа, следует ли делать переносы в словах, надо ли выравнивать текст по левому или правому краю). Команды представляют собой специальные последовательности символов той же кодировки, в которой набран и основной текст.
Отформатированные таким образом тексты могут генерироваться как вручную (например, LATEX ориентирован именно на ручной набор текста), так и различными автоматизированными средствами.
Представление звуков
Представление звуков
Два основных подхода к хранению звуковых файлов можно сопоставить с векторным и растровым способами хранения изображений: это MIDI и подобные ему форматы, и оцифрованный звук.
В формате MIDI звук генерируется синтезатором, который умеет порождать звуки различного тембра, высоты, длительности и громкости. Тембры этих звуков обычно более или менее соответствуют звукам распространенных музыкальных инструментов. Вместо собственно звука хранится последовательность команд этого синтезатора. Используя в качестве звуковых примитивов фонемы человеческого языка, этот подход можно применить и для синтеза речи.
MIDI-файлы имеют малый объем и, при наличии аппаратного синтезатора, не требуют ресурсов центрального процессора для воспроизведения, поэтому их часто используют в качестве фонового озвучивания игровых программ и Web-страниц. К недостаткам этого формата следует отнести тот факт, что качество его воспроизведения определяется качеством синтезатора, которое у дешевых звуковых карт оставляет желать лучшего, и то, что далеко не всякий звук можно воспроизвести таким способом.
Задача преобразования реального звука в MIDI сродни задаче векторизации растрового изображения и другим задачам распознавания образов, и в общем виде не разрешима.
Оцифрованный звук, напротив, является результатом простого осуществления аналого-цифрового преобразования реального звука. Характеристиками такого звука являются частота дискретизации, разрешение АЦП и количество каналов — моно или стерео.
Сложение двух 8разрядных чисел (83 + 56 = 139)
Пример 1.1. Сложение двух 8-разрядных чисел (83 + 56 = 139)
| 1 | 1 | перенос | |||||||
| + | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1-е слагаемое |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое | |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | результат |
Вычитание чисел (83 — 56 = 27)
Пример 1.2. Вычитание чисел (83 — 56 = 27)
Построение двоичного дополнения 56 :
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | число |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | побитовое отрицание |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | побитовое отрицание+1 |
Сложение с двоичным дополнением (83 + 56) mod 256 = 27:
| 1 | 0 | |||||||
| + | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
Из примера видно, что эквивалентность между операциями неполная: сложение с дополнением сопровождается переносом в 9-й разряд, которого нет при прямом вычитании. Этот факт приводит к тому, что мы уже не можем считать перенос в 9-й разряд критерием того, что результат сложения не может быть представлен 8-ю битами. Точный критерий переполнения для целочисленных операций сложения и вычитания теперь звучит так: переполнение произошло, если перенос в 9-й бит (для 8-разрядного АЛУ) не равен переносу в 10-й бит.
Но в остальном двоичное дополнение сильно упрощает жизнь проектировщикам процессоров: вместо двух устройств, сумматора и дифференциатора (по-русски, сложителя и вычитателя), нам достаточно иметь только сумматор. Кроме того, можно представлять отрицательные числа в двоично-дополнительном коде (табл. 1.3). При таком представлении признак переполнения называют также признаком потери знака.
Видно, что четыре бита позволяют нам представить либо ноль и натуральные числа от 1 до 15, либо целые числа от - 8 до 7. Во втором случае, старший бит может интерпретироваться как знаковый — если он равен 1, число отрицательное, если 0 — положительное. Для манипулирования числами в обоих представлениях можно использовать одни и те же команды сложения и вычитания, различие возникает только, когда мы начинаем интерпретировать результаты сравнения таких чисел или сами эти числа (например, переводить их в десятичный формат).
Для команд умножения и деления трюк с двоичным дополнением не проходит, поэтому процессоры, использующие такое представление данных, вынуждены иметь по две пары команд умножения и деления, знаковые и беззнаковые. Любознательному читателю предлагается самостоятельно Разработать алгоритмы умножения и деления двоичных чисел в двоично-Дополнительном представлении. За основу для этих алгоритмов опять-таки рекомендуется взять школьные методы умножения и деления многозначных чисел "в столбик".
Растровое изображение
Рисунок 1.7. Растровое изображение

Наиболее широко используемые цветовые модели — это RGB (Red, Green, Blue — красный, зеленый, синий, соответствующие максимумам частотной характеристики светочувствительных пигментов человеческого глаза), CMY (Cyan, Magenta, Yellow — голубой, пурпурный, желтый, дополнительные к RGB) и CMYG — те же цвета, но с добавлением градаций серого. Цветовая модель RGB используется в цветных кинескопах и видеоадаптерах, CMYG — в цветной полиграфии.
В различных графических форматах используется разный способ хранения пикселов. Два основных подхода — хранить числа, соответствующие пикселам, одно за другим, или разбивать изображение на битовые плоскости -сначала хранятся младшие биты всех пикселов, потом — вторые и так далее. Обычно растровое изображение снабжается заголовком, в котором указано его разрешение, глубина пиксела и, нередко, используемая цветовая модель.
Система Вернама
Рисунок 1.10. Система Вернама
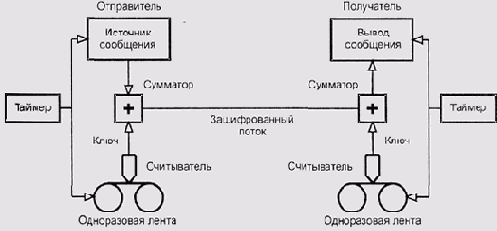
Если ключ порожден надежным генератором случайных чисел (например, правильно настроенным оцифровщиком теплового шума), никакая информация об автокорреляциях в исходном тексте сообщения взломщику не поможет: перебирая полное пространство ключей, взломщик вынужден будет проверить все сообщения, совпадающие по количеству символов с исходным, в том числе и все сообщения, удовлетворяющие предполагаемому автокорреляционному соотношению.
Это преимущество теряется, если один и тот же ключ будет использован для кодирования нескольких сообщений: взломщик, перехвативший их все, сможет использовать эти сообщения и предположения об их содержимом при попытках отфильтровать ключ от полезной информации — отсюда и второе название алгоритма. Применение системы Вернама, таким образом, сопряжено с дорогостоящей генерацией и, главное, транспортировкой ключей огромной длины, и поэтому она используется лишь в системах экстренной правительственной и военной связи.
Более практичным оказалось применение в качестве ключа псевдослучайных последовательностей, порождаемых детерминированными алгоритмами. В промежутке между первой и второй мировыми войнами широкое распространение получили шифровальные машины, основанные на механических генераторах таких последовательностей. Чаще всего использовались сочетания, получаемые при вращении колес с взаимно простыми количествами зубцов.
Основной опасностью при использовании таких методов шифрования является возможность определить текущую точку последовательности — узнав ее (например, по косвенным признакам догадавшись, что в данной точке сообщения должно быть такое-то слово, и восстановив использовавшийся при ее шифровании элемент ключа), взломщик может продолжить генерацию с той же точки и расшифровать весь дальнейший поток.
В системах цифровой связи широкое применение получили блочные алгоритмы, выполняющие над блоками данных фиксированной длины последовательности -- иногда довольно сложные — перестановок, подстановок и других операций, чаще всего двоичных сложений данных с ключом по какому-либо модулю. В операциях используются компоненты ключевого слова относительно небольшой разрядности.
Например, широко применяемый блочный алгоритм DES шифрует 64-битные блоки данных 56-битным ключом. Полное описание алгоритма приводится в документе [NBS FIPS PUB 46, 1977]. Русский перевод этого документа может быть найден в приложениях к книге [Дейтел 1987]. Для современной вычислительной техники полный перебор 56-битного пространства — "семечки", поэтому сейчас,все большее распространение получают алгоритмы с большей разрядностью ключа — Blowfish, IDEAL и др. [Анин 2000].
Шифры с открытым ключом называются также двухключевыми. Если в алгоритмах со скрытым ключом для кодирования и декодирования сообщений используется один и тот же ключ, то здесь используются два ключа: публичный и приватный. Для прочтения сообщения, закодированного публичным ключом, необходим приватный, и наоборот.
Помимо обычных соображений криптостойкости, к таким алгоритмам предъявляется дополнительное требование: невозможность восстановления приватного ключа по публичному иначе как полным перебором пространства ключей.
Двухключевые схемы шифрования намного сложнее в разработке, чем схемы с секретным ключом: требуется найти преобразование, не поддающееся обращению при помощи применявшегося в нем публичного ключа, но такое, чтобы с применением приватного ключа его все-таки можно было обратить. Известные криптоустойчивые схемы основаны на произведениях простых чисел большой разрядности, дискретных логарифмах и эллиптических кривых. Наиболее широкое применение получил разработанный в 1977 г. алгоритм RSA
Таблица сложения одноразрядных двоичных чисел
Таблица 1.1. Таблица сложения одноразрядных двоичных чисел
| 0 + 0 = 00 |
| 0+1 =01 |
| 1+0 = 01 |
| 1 + 1 = 10 |
Из табл. 1.1 видно, что результат сложения двух одноразрядных чисел является двухразрядным (двузначным) числом, а результат сложения двух N-разрядных — N+1 -разрядным. Образующийся дополнительный бит называется битом переноса (carry bit).
При сложении двоичных чисел в столбик мы выписываем их друг под другом (пример 1.1). Два младших разряда мы складываем в соответствии с табл. 1.1. При сложении последующих двух разрядов мы должны учитывать не только эти разряды, но и бит переноса из младшего разряда, т. е. производить сложение в соответствии с табл. 1.2. Из этой таблицы видно, что для трех одноразрядных слагаемых все равно получается только два бита суммы, так что для работы со всеми последующими разрядами мы можем обойтись только одним битом переноса (Рисунок 1.1).
Таблица сложения с учетом переноса
Таблица 1.2. Таблица сложения с учетом переноса
| 0+0+0=0 |
| 0+1+0=01 |
| 1+0+0=01 |
| 0+0+1=01 |
| 1+1+0=10 |
| 1+0+1=10 |
| 0+1+1=10 |
| 1+1+1=11 |
Двоичное представление
Таблица 1.3. Двоичное представление знаковых и беззнаковых чисел
| Беззнаковое | Знаковое | Двоичное |
| 7 | +7 | 0111 |
| 6 | +6 | 0110 |
| 5 | +5 | 0101 |
| 4 | +4 | 0100 |
| 3 | +3 | 0011 |
| 2 | +2 | 0010 |
| 1 | +1 | 0001 |
| 0 | 0 | 0000 |
| 15 | -1 | 1111 |
| 14 | -2 | 1110 |
| 13 | -3 | 1101 |
| 12 | -4 | 1100 |
| 11 | -5 | 1011 |
| 10 | -6 | 1010 |
| 9 | -7 | 1001 |
| 8 | -8 | 1000 |
Подавляющее большинство современных процессоров использует двоично-дополнительное представление для целых чисел. В те времена, когда компьютеры были большими, встречались системы, применявшие для этой цели дополнительный, знаковый бит: число —1 представлялось так же, как +1, но с установленным знаковым битом. Такие процессоры должны были иметь отдельные команды для беззнаковых и знаковых арифметических операций и более сложное АЛУ. Кроме того, при таком представлении возникает специфическая проблема "отрицательного нуля".
Иногда наравне с двоичным используется и специфическое, так называемое двоично-десятичное представление чисел (Рисунок 1.2). Это представление особенно удобно для приложений, которые постоянно вынуждены использовать десятичный ввод и вывод (микрокалькуляторы, часы, телефоны с автоопределителем номера и т. д.) и имеют небольшой объем программной памяти, в который нецелесообразно помещать универсальную процедуру преобразования чисел из двоичного представления в десятичное и обратно.
В таком представлении десятичная цифра обозначается тетрадой, четырьмя битами. Цифры от 0 до 9 представляются 0, 1111 недопустимы.своими двоичными эквивалентами, а комбинации битов 1010, 1011, 1100, 1101, 111
Русская азбука Морзе
Таблица 1.4. Русская азбука Морзе
| Буква |
Символы Морзе |
Слово |
Буква |
Символы Морзе |
Слово |
| А |
.- |
а-том |
Р |
.-. |
ра-ду-га |
| Б |
-... |
бес-са-раб-ка |
С |
са-ма-ра |
|
| В |
.-- |
ва-ви-лон |
Т |
- |
Ток |
| Г |
--. |
го-ло-ва |
У |
..- |
|
| Д |
-.. |
до-бав-ка |
ф |
..-. |
фа-на-тич-ка |
| Е |
X |
ха-на-ан-ка |
|||
| Ж |
...- |
жат-ва-зла-ков |
ц |
-.-. |
цы-га-ноч-ка |
| 3 |
--.. |
звон-бу-ла-та |
ч |
че-ре-му-ха |
|
| И |
ш |
— - |
ше-ре-ме-тев |
||
| К |
-.- |
конс-тан-тин |
Щ |
--.- |
щу-ро-гла-зый |
| Л |
.-.. |
ла-до-жан-ка |
ю |
..-- |
|
| М |
-- |
ми-иин |
я |
.-.- |
|
| Н |
-. |
но- га |
ы |
-.-- |
ы-ка-ни-е |
| 0 |
— |
о-ло-во |
ь-ъ |
-..- |
|
| П |
.--. |
па-ни-хи-да |
Примечание
Примечание
Во вспомогательных словах для запоминания слоги, содержащие букву "а", обозначают точкой, не содержащие - тире.
В конце сороковых годов XX века основателем современной теории информации Шенноном, и независимо от него, Фано был разработан универсальный алгоритм построения оптимальных кодов. Более известый аналог этого алгоритма был предложен несколько позже Дэвидом Хаффманом [Huffman 1952]. Принцип построения этих кодов в целом соответствует логике, которой руководствовался Морзе, — кодировать значения, которые часто повторяются в потоке, более короткими последовательностями битов.
Коды Хаффмана и Шеннона-Фано устраняют автокорреляции, соответствующие неравномерности встречаемости символов, но сохраняют без изменений часто встречающиеся последовательности символов, а они ответственны за значительную часть избыточности текстов на естественных и синтетических языках. Для упаковки данных такого рода в конце 70-х Лемпелем и Зиффом было предложено семейство алгоритмов, наиболее известные из которых - LZ77 и LZW [Lempel-Ziv 1978].
Все эти алгоритмы сводятся к поиску в потоке повторяющихся последовательностей и замене этих последовательностей на их номер в динамически формируемом словаре. Различие состоит в способах кодирования номера и формирования словаря. Номер последовательности в словаре должен содержать больше битов, чем символы исходного потока, хотя бы уже для того, чтобы его можно было отличить от символа, поэтому алгоритмы Лемпеля-Зиффа предполагают дальнейшее перекодирование преобразованного потока кодом Хаффмана. Большинство современных архиваторов, такие, как PkZip, GNU Zip, RAR, основаны на вариациях и аналогах алгоритмов Лем-пеля-Зиффа.
При упаковке нетекстовых данных могут применяться и другие способы удаления повторений. Например, при упаковке растровых изображений широко используется метод RLE (Run-Length Encoding), когда повторяющиеся пикселы заменяются счетчиком повторений и значением пиксела.
Наиболее универсальны так называемые арифметические алгоритмы, которые находят и устраняют все автокорреляции, присутствующие во входных данных. Математическое обоснование и принципы работы этих алгоритмов заслуживают отдельной книги и увели бы нас далеко в сторону от темы. К сожалению, из-за больших вычислительных затрат эти алгоритмы и реализующие их программы не получают широкого распространения.
Все перечисленные алгоритмы способны только устранять автокорреляции, уже существующие во входном потоке. Понятно, что если автокорреляций не было, то упаковки не произойдет, поэтому гарантировать уровень упаковки эти алгоритмы не могут.
Для упаковки данных, полученных оцифровкой реальных сигналов, прежде всего изображений и звука, точные алгоритмы не подходят совершенно. Дело в том, что реальный сигнал всегда сопровождается тепловым, так называемым белым (равномерно содержащим все частоты) шумом. Этот шум искажает наличествующие в сигнале автокорреляции, сам же автокорреляций не имеет, поэтому обратимые алгоритмы с зашумленным сигналом справиться не могут.
Чтобы убедиться в этом, можно попробовать упаковать любым, или даже несколькими из распространенных архиваторов трек аудио-CD или цифровую фотографию впрочем, чтобы с цифровой фотографией фокус получился, необходимо, чтобы кадр был снят без обработки встроенным упаковщиком камеры.
Идея обширного семейства алгоритмов, пригодных для сжатия зашумлен-ных сигналов, была позаимствована из принципа работы цифровых фильт-ров-"щумодавов". Шумодав работает следующим образом: он осуществляет над сигналом преобразование Фурье и удаляет из полученного спектрального образа самые слабые частоты, которые ниже порога подавления.
Сигнал при этом, конечно, искажается, но сильнее всего при этом страдает равномерно распределенный по спектру шум, что и требуется (Рисунок 1.8).
Трехмерное векторное изображение
Рисунок 1.6. Трехмерное векторное изображение
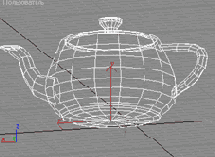
Двухмерные векторные форматы очень хороши для-представления чертежей, диаграмм, шрифтов (или, если угодно, отдельных букв шрифта) и отформатированных текстов. Такие изображения удобно редактировать — изображения и их отдельные элементы легко поддаются масштабированию и другим преобразованиям. Примеры двухмерных векторных форматов — PostScript, PDF (Portable Document Format, специализированное подмножество PostScript), WMF (Windows MetaFile), PCL (Printer Control Language, система команд принтеров, поддерживаемая большинством современных лазерных и струйных печатающих устройств). Примером векторного представления движущихся изображений является MacroMedia Flash. Трехмерные векторные форматы широко используются в системах автоматизированного проектирования и для генерации фотореалистичных изображений методами трассировки лучей и т. д.
Однако преобразование реальной сцены (например, полученной оцифровкой видеоизображения или сканированием фотографии) в векторный формат представляет собой сложную и, в общем случае, неразрешимую задачу. Программы-векторизаторы существуют, но потребляют очень много ресурсов, а качество изображения во многих случаях получается низким. Самое же главное — создание фотореалистичных (фотографических или имитирующих фотографию) изображений в векторном формате, хотя теоретически и, возможно, на практике требует большого числа очень сложных примитивов. Гораздо более практичным для этих целей оказался другой подход к оцифровке изображений, который использует большинство современных устройств визуализации: растровые дисплеи и многие печатающие устройства.
В растровом формате изображение разбивается на прямоугольную матрицу элементов, называемых пикселами (слегка искаженное PICture ELement — этемент картинки). Матрица называется растром. Для каждого пиксела определяется его яркость и, если изображение цветное, цвет. Если, как это часто бывает при оцифровке реальных сцен или преобразовании в растровый формат (растеризации) векторных изображений, в один пиксел попали несколько элементов, их яркость и цвет усредняются с учетом занимаемой площади. При оцифровке усреднение выполняется аналоговыми контурами аналого-цифрового преобразователя, при растеризации — алгоритмами анти-алиасинга.
Размер матрицы называется разрешением растрового изображения. Для печатающих устройств (и при растеризации изображений, предназначенных для таких устройств) обычно задается неполный размер матрицы, соответствующей всему печатному листу, а количество пикселов, приходящихся на вертикальный или горизонтальный отрезок длиной 1 дюйм; соответствующая единица так и называется — точки на дюйм (DPI, Dots Per Inch).
Для черно-белой печати обычно достаточно 300 или 600 DPI. Однако принтеры, в отличие от растровых терминалов, не умеют манипулировать яркостью отдельной точки, поэтому изменения яркости приходится имитировать, разбивая изображение на квадратные участки и регулируя яркость относительным количеством черных и белых (или цветных и белых при цветной печати) точек в этом участке. Для получения таким способом приемлемого качества фотореалистичных изображений 300 DPI заведомо недостаточно, и даже бытовым принтерам приходится использовать гораздо более высокие разрешения, вплоть до 2400 DPI.
Вторым параметром растрового изображения является разрядность одного пиксела, которую называют цветовой глубиной. Для черно-белых изображений достаточно одного бита на пиксел, для градаций яркости серого или цветовых составляющих изображения необходимо несколько битов (Рисунок 1.7). В цветных изображениях пиксел разбивается на три или четыре составляющие, соответствующие разным цветам спектра. В промежуточных данных, используемых при оцифровке и редактировании растровых изображений, цветовая глубина достигает 48 или 64 бит (16 бит на цветовую составляющую). Яркостный диапазон современных Мониторов, впрочем, позволяет ограничиться 8-ю битами, т. е. 256 градациями, на одну цветовую составляющую: большее количество градаций просто незаметно глазу.
Упаковка данных
Упаковка данных
Данные многих форматов имеют значительный объем, поэтому их хранение и передача зачастую требуют значительных ресурсов. Одним из способов решения этой проблемы является повышение емкости запоминающих устройств и пропускной способности каналов связи. Однако во многих случаях применима и более дешевая альтернатива этим методам — упаковка данных.
Научной основой всех методов упаковки является теория информации: данные, в которых имеются статистические автокорреляции, называются избыточными или имеющими низкую энтропию. Устранив эти автокорреляции, т. е. повысив энтропию, объем данных можно уменьшить без потери смысла, а зачастую и с возможностью однозначно восстановить исходные данные. Методы повышения энтропии, которые не позволяют по упакованному потоку восстановить исходный, называются необратимыми, приблизительными или сжимающими с потерями (losing compression). Соответственно, методы, которые позволяют это сделать, называются обратимыми, точными, или сжимающими без потерь (losless compression).
Один из первых методов упаковки был предложен задолго до разработки современной теории информации; в 1844 году Сэмюэл Морзе построил первую линию проволочного телеграфа. Система кодировки букв, известная как Азбука Морзе (табл. 1.4), использовала для представления различных букв алфавита посылки различной длины, при этом длина посылки зависела от частоты использования соответствующего символа в английском языке. Часто встречающиеся символы кодировались более короткими последовательностями.
Введение в двоичную арифметику
Введение в двоичную арифметику
| А для такой низкой жизни были числа, Как домашний, подъяремный скот Потому, что все оттенки смысла Умное число передаст Н. Гумилев |
Арифметические операции над двоичными числами осуществляются при помощи алгоритма, который в школе изучают под названием "сложение в столбик".
Введение в криптографию
Введение в криптографию
| Список замеченных опечаток: В шифровке на стр. 325 напечатано: 212850А Следует читать: 212850Б |
При хранении и передаче данных нередко возникает требование защитить их от нежелательного прочтения и/или модификации. Если задача защиты от нежелательной модификации решается обсуждавшимися в предыдущем разделе избыточными кодами, то с прочтением все существенно сложнее.
Проще всего обеспечить защиту данных, лишив потенциальных злоумышленников доступа к физическому носителю данных или физическому каналу, по которому происходит их передача. К сожалению, иногда это невыполнимо (например, если обмен данными происходит по радиоканалу), а зачастую просто слишком дорого. В этом случае на помощь приходят методики, собирательное название которых — криптография (тайнопись). В отличие от большинства терминов компьютерной лексики это слово не английского, а греческого происхождения.
История криптографии насчитывает тысячи лет, и многие основополагающие принципы современной криптографии известны, возможно, с доисторических времен, однако, существенный прогресс в теории шифрования был достигнут лишь относительно недавно, в связи с разработкой современной теории информации.
Практически все методы криптографии сводятся к преобразованию данных в набор из конечного количества символов и осуществлению над этими символами двух основных операций: подстановки и перестановки. Подстановка состоит в замене одних символов на другие. Перестановка состоит в изменении порядка символов. В качестве символов при этом могут выступать различные элементы сообщения — так, при шифровании сообщений на естественных языках подстановке и перестановке могут подвергаться как отдельные буквы, так и слова или даже целые предложения (как, например, в аллегорических изложениях магических и священных текстов). В современных алгоритмах этим операциям чаще всего подвергаются блоки последовательных битов. Некоторые методики можно описать как осуществление операции подстановки над полным сообщением.
Подстановки и перестановки производятся по определенным правилам. При этом надежда возлагается "на то, что эти правила и/или используемые в них параметры известны только автору и получателю шифрованного сообщения и неизвестны посторонним лицам. В докомпьютерную эру старались засекретить обе составляющие процесса шифрования. Сейчас для шифрования, как правило, используют стандартные алгоритмы, секретность же сообщения достигается путем засекречивания используемого алгоритмом параметра, ключа (key).
Прочтение секретного сообщения посторонним лицом, теоретически, может быть осуществлено двумя способами: похищением ключевого значения либо его угадыванием путем анализа перехваченной шифровки. Если первое мероприятие может быть предотвращено только физической и организационной защитой, то возможность второго определяется используемым алгоритмом. Ниже мы будем называть процесс анализа шифровки взломом шифра, а человека, осуществляющего этот процесс, — взломщиком. По-научному эта деятельность называется более нейтрально — криптоанализ.
К примеру, сообщение на естественном языке, зашифрованное подстановкой отдельных букв, уязвимо для частотного анализа: основываясь на том факте, что различные буквы встречаются в текстах с разной частотой, взломщик легко- и с весьма высокой достоверностью- может восстановить таблицу подстановки. Существуют и другие примеры неудачных алгоритмов, которые сохраняют в неприкосновенности те или иные присутствовавшие в сообщении автокорреляции — каждый такой параметр можно использовать как основу для восстановления текста сообщения или обнаружения ключа.
Устойчивость шифра к поиску автокорреляций в сообщении называется криптостойкостыо алгоритма. Даже при использовании удачных в этом смысле алгоритмов, если взломщик знает, что исходные (нешифрованные) данные удовлетворяют тому или иному требованию, например, содержат определенное слово или снабжены избыточным кодом, он может произвести полный перебор пространства ключей: перебирать все значения ключа, допускаемые алгоритмом, пока не будет получено удовлетворяющее требованию сообщение. При использовании ключей достаточно большой разрядности такая атака оказывается чрезмерно дорогой, однако прогресс вычислительной техники постоянно сдвигает границу "достаточности" все дальше и дальше. Так, сеть распределенных вычислений Bovine в 1998 году взломала сообщение, зашифрованное алгоритмом DES с 56-разрядным ключом за 56 часов работы
Зашумленный сигнал и его спектральный
Рисунок 1.8. Зашумленный сигнал и его спектральный образ (результат преобразования Фурье), цит. по [Smith 1997]
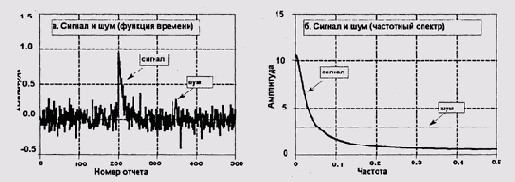
Алгоритмы JFIF (лежащий в основе распространенного формата хранения растровых изображений JPG), MPEG, MP3 [www.jpeg.org] тоже начинаются с выполнения над входным потоком преобразования Фурье. Но, в отличие от шумодава, JFIF удаляет из полученного спектра не частоты, которые ниже заданного порога, а фиксированное количество частот — конечно же, стараясь отобрать самые слабые. Количество частот, которые надо выкинуть, определяется параметром настройки упаковщика. У JFIF этот параметр так и называется — коэффициентом упаковки, у МРЗ — битрейтом.
Профильтрованный сигнал заведомо содержит автокорреляции — даже если исходный, незашумленный, сигнал их и не содержал, такая фильтрация их создаст — и потому легко поддается упаковке. Благодаря этому, все перечисленные алгоритмы обеспечивают гарантированный уровень упаковки. Они способны сжать в заданное число раз даже чистый белый шум. Понятно, что точно восстановить по подвергнутому такому преобразованию потоку исходный сигнал невозможно, но такой цели и не ставится, поэтому все перечисленные методы относятся к разряду необратимых.
При разумно выбранном уровне упаковки результат — фотореалистичное изображение или музыкальное произведение — на взгляд (или, соответственно, на слух) практически неотличим от оригинала. Различие может показать только спектральный анализ данных. Но если распаковать сжатое с потерями изображение, подвергнуть его редактированию (например, отмасштабировать или пририсовать какой-нибудь логотип), а потом упаковать снова, результат будет удручающим: редактирование привнесет в изображение новые частоты, поэтому велика опасность, что повторная упаковка даже с более низким коэффициентом сжатия откусит какие-то из "полезных" частот изображения. После нескольких таких перепаковок от изображения остается только сюжет, а от музыки — только основной ритм. Поэтому всерьез предлагается использовать приблизительные алгоритмы упаковки в качестве механизма зашиты авторских прав: в спорной ситуации только настоящий автор произведения может предъявить его исходный, неупакованный вариант.
Экспериментальные варианты приблизительных алгоритмов вместо классического разложения по взвешенной сумме синусов и косинусов используют разложение по специальным функциям, так называемым вэйвлетам (wavelet). Утверждается, что вэйвлетная фильтрация при том же уровне сжатия (понятно, что сравнивать по уровню сжатия алгоритмы, которые сжимают что угодно в заданное число раз, совершенно бессмысленно) дает меньший уровень субъективно обнаружимых искажений. Но субъективное восприятие, как известно, сильно подвержено эффекту плацебо (человек склонен видеть улучшение или вообще изменение там, где его нет, если имеет основания предполагать, что изменение должно произойти), зато вэйвлетные алгоритмы сильно уступают обычным вариациям JFIF по производительности, поэтому до сих пор они не вышли из экспериментального состояния.
